「新しい現象解析法の開発」–１

・“複雑現象を簡潔に解く！”

現場で複雑な現象と日々向き合っている技術者にとっては、「高精度ではあるが中身がいわゆるブラックボックスで、かつ種々の条件による多くの解を得ることは難しい」という方法よりも「多少の精度は犠牲にしても中身が把握できて、しかも種々の条件による多くの解を短期間で得られる」方法の方を望む場合が多い。従来のコンピューターシミュレーションに代表される方法はほぼ例外なく前者の場合であり、高度な専門性と高コストが要求される。なぜ、そのような状況にあるのかを一言でいえば、現象を微分方程式からきっちりと積み上げ、かつ対象体を非常に細かな領域要素の分割するためである。

それに対して、我が社では、前述したような技術者の要望に応えるべく以下の概説する方法を開発し実用に供しつつある。

対象体の形状と領域要素分割を非常にシンプル化するということを行い、その代わりに現象に関与するあらゆるパラメーターを取り込み、そして現象は代数方程式で定式化する。それらの式はいわゆる“非線形・高次の連立式”となる場合が多く、その場合には初等的な方法で解を得ることは難しい。そこで、それらの非線形方程式の解法として“図化近似解法”を開発した。

これらの新しい方法によって、多くの条件点数の組み合わせによる多くの解の点の集合（「解の集合曲面」と呼ぶ）を非常に短時間で求めることができる。そして、その解の集合曲面の性質を紐解くことで、技術者は”対象の現象の全体感“を把握できるとともに、系全体の制御上の情報も見出すことができる。

なお、式は代数方程式から構成されることから、基本的には“エクセル”などによる計算が可能であり、計算の中身も把握しやすく、ブラックボックス化を避けることも可能となる。

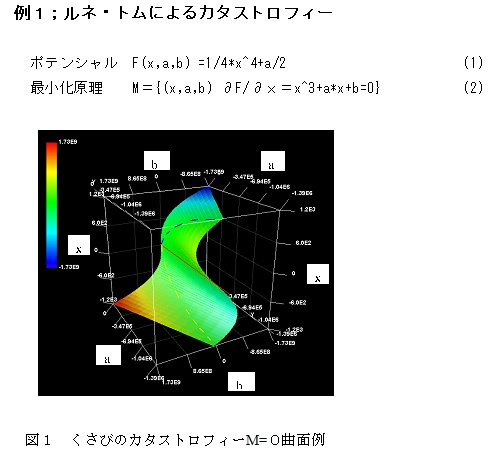
例１；このような図解（トポロジカルな方法と呼ぶ）によってカタストロフィーという不安定現象の解明をルネ・トムが提唱した一例を再現してみた。

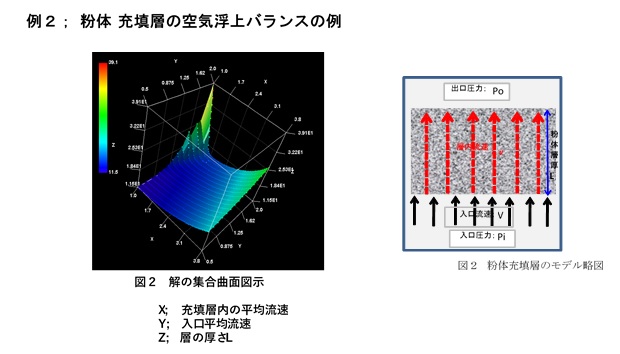
例２；実際の設備をイメージして、気体吹き込みによる粉体充填層の浮上について定式化し、図式解法を適用して得られた解の集合曲面の例を示す。

＊なお作図は、いずれもフリーソフト「RinearnGraph3D」による

 

 

「新しい現象解析法の開発」–２

・“アイソレート（ノードレス）要素解析”

Ⓡ「iSOLEM」6147871

Ⓡ「アイソレート要素法」6147870

コンピューターシミュレーション手法として、現在広く普及している方法は“有限要素法”である。その有限要素法とは、各要素の頂点に「節点」をもうけその点での値を未知のパラメーターとする方法であり、そのパラメーターは、構造解析分野でいえば”変位“である。

しかし、この方法は広く普及してきてはいるが、いまだに次のような問題を抱えている。

・“節点”を設けていることによる種々の弊害

・発生する不自然さを回避するため様々なノウハウを必要とする

特に、構造解析における変位や応力の“正解”の存在の理論的な証明が明確に話されていないと言える。

そこで、弊社ではこれらの問題を解決すべく、「アイソレート（ノードレス）要素法」の開発に取り組んでいる。

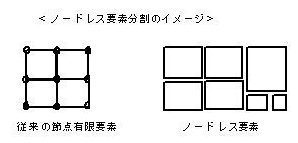
アイソレート（ノードレス）要素法では、従来の有限要素法が、要素間を節点のパラメーターで結合していることに対して、要素間の辺（あるいは面）上の変位や応力による積分値の等価によって結合されている。さらに、従来の有限用要素法が節点の値を求めることに対しアイソレート（ノードレス）要素法では要素内部を級数で定義する場合の未知パラメーターを求める。

アイソレート（ノードレス）要素法の特徴は次のようになる

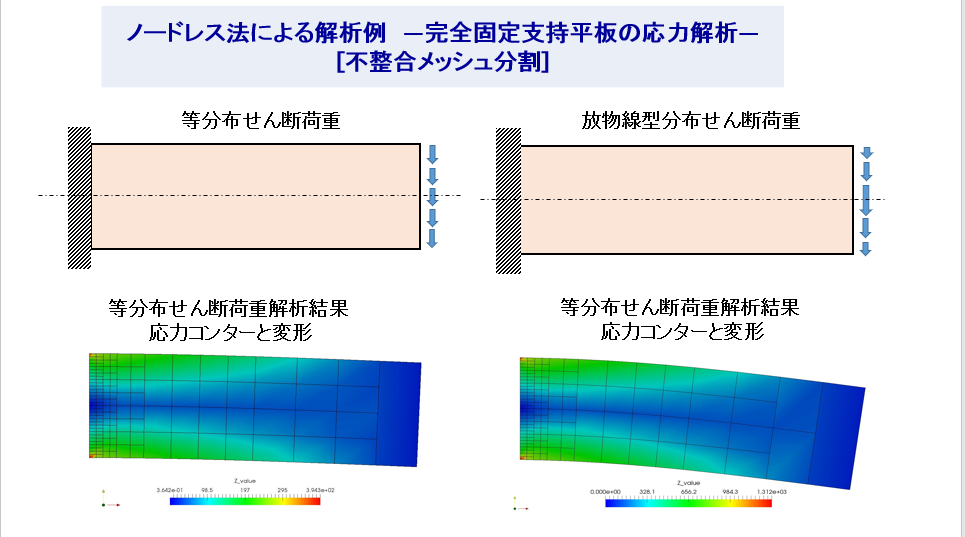
・ ”不整合”なメッシュが可能となり、ズーミングや”中抜き””はめ込み“が容易である。

・　背景となっている理論は「混合法^＊１」でありいわゆる上下界解を計算して上下界解の挟み撃ちで正解の存在範囲を示すことができる。

・　従来の有限要素法のように、変位の精度の確保のために応力の精度が犠牲になることはなく、同等に扱うことができる。

・　各要素に対して、種々の近似関数を近似することができることから、超高周波の振動解析などに威力を発揮する。

・　さらにこれらの特徴から、接触問題や軟らかな物体への応用の拡張が期待できる。

・　計算時間は、問題にもよるがほぼ従来と同等であると予想されるが、並列化の効果を活かすには適している。

 　                        

 

アイソレート（ノードレス）要素解析のよさ                                                                                                                   

・ズーミングアップが容易！（従来FEMではほとんど現実には不可能に近い）

・メッシュの不整合が容易（異形メッシュでもせきぶんさえできればOK)

・メッシュの部分中抜きやはめ込みが可能

・一要素の部分マトリックスをあたかも連立式の係数マトリクスの一係数と同等に扱えるため連立式の解き方になじむ

・要素がつぶれてもよい！・・やわらかいものの扱いとかが自然にできる

・長い間の懸案の接触問題を”合理的に”解析可能

・並列化の効果が引き出せる可能性が高い

・応力法を嘱望する分野には最適である

 

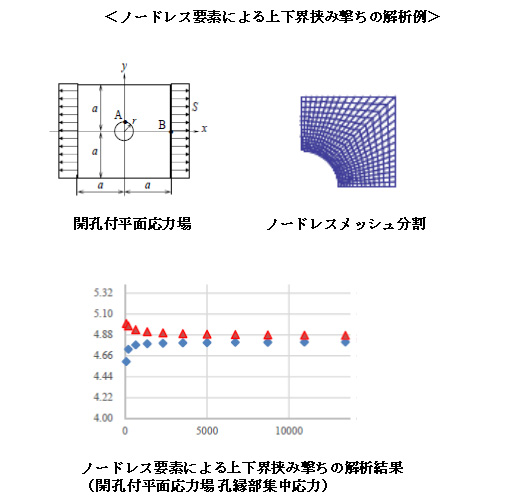
アイソレート要素法による正解の存在保証

 

 

対象の構造体を多数の要素に分割して解析するにあたって、要素数を細かくすれば精度が上がっていくことは容易に予想できる。しかしながら、従来は、いくら細かく要素に分割してもその収束先が正解かどうかの保証、すなわち「正解の存在保証」は困難である。

従来のFEMは、エネルギーを高めに評価しており、得られる解は“上界解”と呼ばれ、多数分割によって正解へ収斂するかどうかの保証はされない。

しかし、開発されたアイソレート要素法を用いて、（構造解析の例で）応力と変位をそれぞれ独立に定義し、高めに評価したエネルギー（上界解）と低めに評価したエネルギー（下界解）の各々から得られる解によって“挟み撃ち”することにより、その間に正解の存在の保証をすることができるようにした。

このことは、”離散的に解く場合の正解の保証“という当分野の長い間の基礎的な課題をクリアする礎となり、数値シミュレーション結果の信頼性を確保するための非常に重要なことであると言えよう。

 

・“アイソレート法による超高周波の固有振動モード解析”

アイソレート要素法は、節点レスのため要素の変位関数を任意に採ることが可能である。よって高次の変位関数を採用することで、比較的少ない要素数で騒音などに関連するｋHzオーダーの高い周波数の固有振動変形モードの解析（固有値解析）が可能です。

従来のFEMですと節点数の制約があり高い周波数の変形モードの解析は実務的にはかなり困難です。

今後、高周波帯における騒音解析等での振動源の特定などに応用が期待され、様々な構造に対応するための要素形状開発を計画しております。

以下に平板の曲げの固有振動解析例を示します。

 

＜計算例＞

モデル；1mx1mx厚さ5mm の平板

材料定数 𝐄=𝟐𝟎𝟗𝐆𝐏𝐚, ν＝0.3，密度𝝆=𝟕𝟗𝟎𝟎𝑲𝒈/𝒎^𝟑

一要素内の撓み関数は6次関数

 

計算結果                                                                

要素数	変形波数*1	固有振動数(Hz)	理論固有振動数(Hz)
8×18＝324	1×1波	24.45	24.45
	4×4波	391.08	391.19
	10×10波	2432.9	2444.9
26×26=676	20×20波	9781.7	9779.8
	24×24波	14,240.7	14,082.9

*1) 変形波数とは振動による変形後の”波”の数を指しており例えば「20×20波」の場合は下図に示すような変形状態を示す。

 

「受託解析や技術コンサルティング」

・“経験を活かした問題解決型の解析技術！”

様々な構造物の強度解析をはじめ、流体や熱の問題など様々な計算機シミュレーションの解析業務の受託が可能です。

計算機シミュレーションのみならず、経験活かして設計や製造、トラブルの原因解析などの問題解決に向けてのアドバイスやコンサルテイングも可能です。

対象とする課題例；

構造物一般の強度解析

タンクなどの構造物の破損原因解明

溶接構造物の残留応力や変形の解析

曲げやプレス加工のシミュレーション

き裂の進展解析

伝熱解析

熱による変形や破損の解析

対象とする材料は金属の他プラスチック、コンクリート、岩盤なども可能

流体の解析

機械振動や地震動解析

繰り返し疲労解析